【2022-09-16每日一题】850. 矩形面积 II
2022-09-16
2分钟阅读时长
2022-09-16每日一题:850. 矩形面积 II
- 难度:Hard
- 标签:线段树 、 数组 、 有序集合 、 扫描线
我们给出了一个(轴对齐的)二维矩形列表 rectangles 。 对于 rectangle[i] = [x1, y1, x2, y2],其中(x1,y1)是矩形 i 左下角的坐标, (xi1, yi1) 是该矩形 左下角 的坐标, (xi2, yi2) 是该矩形 右上角 的坐标。
计算平面中所有 rectangles 所覆盖的 总面积 。任何被两个或多个矩形覆盖的区域应只计算 一次 。
返回 总面积 。因为答案可能太大,返回 109 + 7 的 模 。
示例 1:
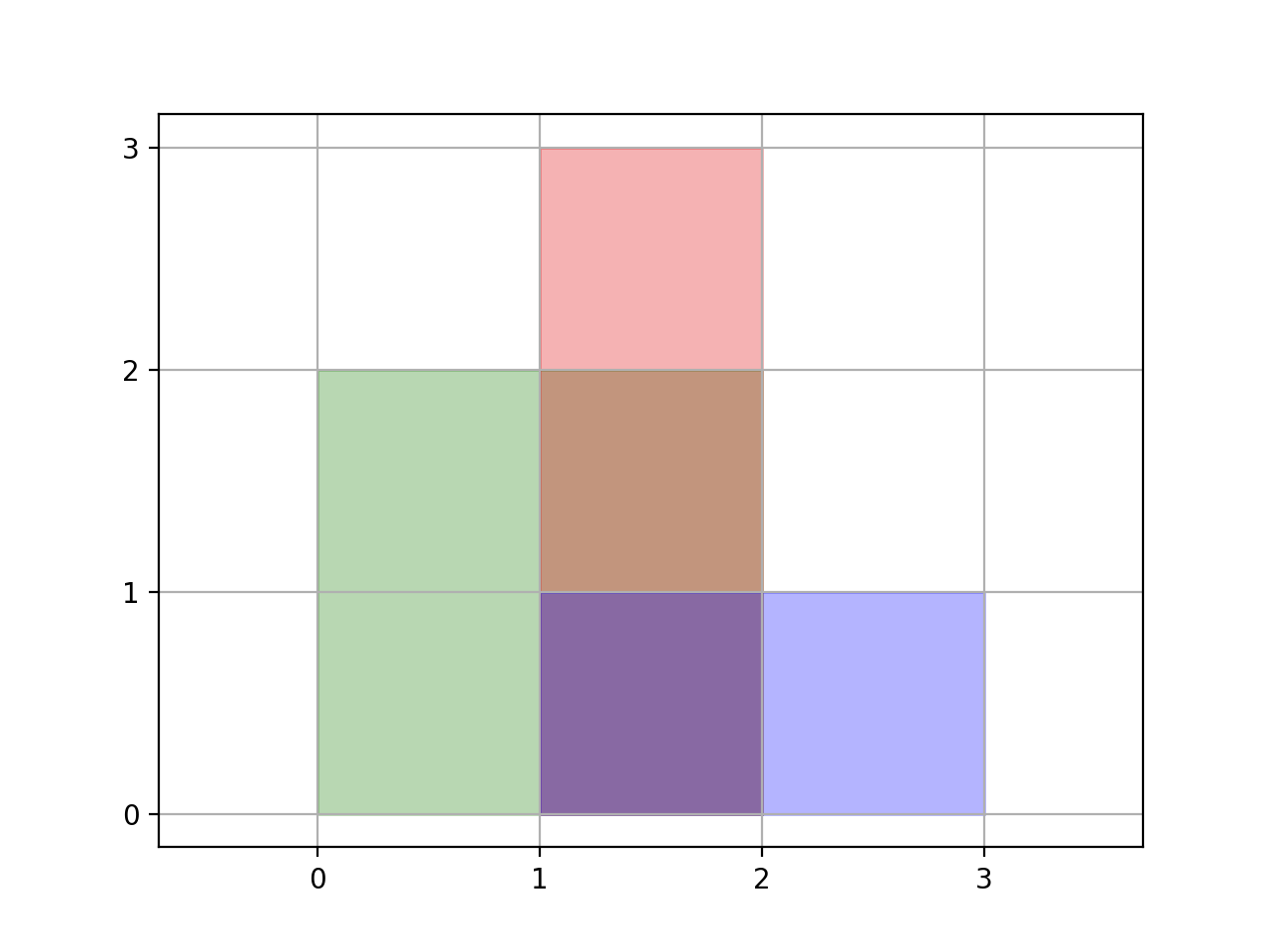
输入:rectangles = [[0,0,2,2],[1,0,2,3],[1,0,3,1]] 输出:6 解释:如图所示,三个矩形覆盖了总面积为6的区域。 从(1,1)到(2,2),绿色矩形和红色矩形重叠。 从(1,0)到(2,3),三个矩形都重叠。
示例 2:
输入:rectangles = [[0,0,1000000000,1000000000]] 输出:49 解释:答案是 1018 对 (109 + 7) 取模的结果, 即 49 。
提示:
1 <= rectangles.length <= 200rectanges[i].length = 40 <= xi1, yi1, xi2, yi2 <= 109- 矩形叠加覆盖后的总面积不会超越
2^63 - 1,这意味着可以用一个 64 位有符号整数来保存面积结果。
方法一:
详细思路过程见宫水三叶题解,这里只做个人刷题记录,方便后续查询阅读
【宫水三叶】扫描线模板题 golang实现
func rectangleArea(rectangles [][]int) (ans int) {
list := make([]int, 0, len(rectangles)*2)
for _, rectangle := range rectangles {
list = append(list, rectangle[0], rectangle[2])
}
sort.Ints(list)
for i := 1; i < len(list); i++ {
a, b := list[i-1], list[i]
width := b - a // x轴宽度
lines := [][2]int{}
for _, rectangle := range rectangles {
if rectangle[0] <= a && b <= rectangle[2] {
lines = append(lines, [2]int{rectangle[1], rectangle[3]})
}
}
// 升序排列
sort.Slice(lines, func (i, j int) bool {
if lines[i][0] != lines[j][0] {
return lines[i][0] <= lines[j][0]
} else {
return lines[i][1] <= lines[j][1]
}
})
total, low, high := 0, -1, -1
for _, line := range lines {
if line[0] > high {
total += high - low
low, high = line[0], line[1]
} else if line[1] > high {
high = line[1]
}
}
total += high - low // y轴总高度
ans += width * total
ans %= 1e9 + 7
}
return ans
}
复杂度分析
时间复杂度:预处理所有扫描线的复杂度为O(nlogn);处理所有相邻的扫描线,并计算相邻扫描线形成的矩形面积复杂度为 O(nlogn) 。整体复杂度为 O(n^2*logn)
空间复杂度:O(n)