【2022-11-09每日一题】764. 最大加号标志[Medium]
2022-11-09
3分钟阅读时长
2022-11-09每日一题:764. 最大加号标志
难度:Medium
标签:数组 、 动态规划
在一个 n x n 的矩阵 grid 中,除了在数组 mines 中给出的元素为 0,其他每个元素都为 1。mines[i] = [xi, yi]表示 grid[xi][yi] == 0
返回 grid 中包含 1 的最大的 轴对齐 加号标志的阶数 。如果未找到加号标志,则返回 0 。
一个 k 阶由 1 组成的 “轴对称”加号标志 具有中心网格 grid[r][c] == 1 ,以及4个从中心向上、向下、向左、向右延伸,长度为 k-1,由 1 组成的臂。注意,只有加号标志的所有网格要求为 1 ,别的网格可能为 0 也可能为 1 。
示例 1:
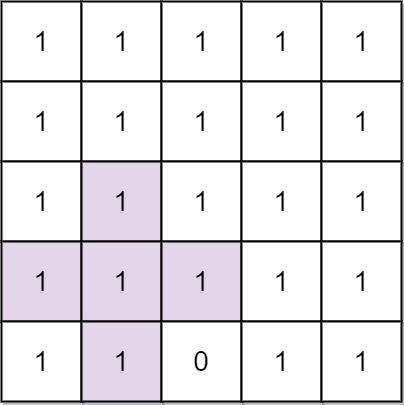
输入: n = 5, mines = [[4, 2]] 输出: 2 解释: 在上面的网格中,最大加号标志的阶只能是2。一个标志已在图中标出。
示例 2:

输入: n = 1, mines = [[0, 0]] 输出: 0 解释: 没有加号标志,返回 0 。
提示:
1 <= n <= 5001 <= mines.length <= 50000 <= xi, yi < n- 每一对
(xi, yi)都 不重复
方法一:动态规划
写法一:
func orderOfLargestPlusSign(n int, mines [][]int) int {
// 初始化
dp := make([][]int, n)
for i := range dp {
dp[i] = make([]int, n)
for j := range dp[i] {
dp[i][j] = n
}
}
// 填充 mines
for _, e := range mines {
dp[e[0]][e[1]] = 0
}
// 处理dp
for i := 0; i < n; i++ {
var left, right, up, down int
for j, k := 0, n-1; j < n; j, k = j+1, k-1 {
left, right, up, down = left+1, right+1, up+1, down+1
if dp[i][j] == 0 {
left = 0
}
if dp[i][k] == 0 {
right = 0
}
if dp[j][i] == 0 {
up = 0
}
if dp[k][i] == 0 {
down = 0
}
dp[i][j] = min(dp[i][j], left)
dp[i][k] = min(dp[i][k], right)
dp[j][i] = min(dp[j][i], up)
dp[k][i] = min(dp[k][i], down)
}
}
// 获取最大值
ans := 0
for i := range dp {
for _, x := range dp[i] {
ans = max(ans, x)
}
}
return ans
}
// 辅助函数
func min(a, b int) int {
if a < b {
return a
}
return b
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
写法二:
func orderOfLargestPlusSign(n int, mines [][]int) (ans int) {
dp := make([][]int, n)
for i := range dp {
dp[i] = make([]int, n)
for j := range dp[i] {
dp[i][j] = n
}
}
banned := map[int]bool{}
for _, p := range mines {
banned[p[0]*n+p[1]] = true
}
// 预处理
for i := 0; i < n; i++ {
count := 0
/* left */
for j := 0; j < n; j++ {
if banned[i*n+j] {
count = 0
} else {
count++
}
dp[i][j] = min(dp[i][j], count)
}
count = 0
/* right */
for j := n - 1; j >= 0; j-- {
if banned[i*n+j] {
count = 0
} else {
count++
}
dp[i][j] = min(dp[i][j], count)
}
}
for i := 0; i < n; i++ {
count := 0
/* up */
for j := 0; j < n; j++ {
if banned[j*n+i] {
count = 0
} else {
count++
}
dp[j][i] = min(dp[j][i], count)
}
count = 0
/* down */
for j := n - 1; j >= 0; j-- {
if banned[j*n+i] {
count = 0
} else {
count++
}
dp[j][i] = min(dp[j][i], count)
ans = max(ans, dp[j][i])
}
}
return ans
}
func min(a, b int) int {
if a > b {
return b
}
return a
}
func max(a, b int) int {
if b > a {
return b
}
return a
}
复杂度分析
时间复杂度:O(n^2),其中 n 表示矩阵的行数。我们最多需要遍历 4 次即可计算出每个点上的 4 方向上连续 1 的最大数目,因此需要的时间为 O(n^2)。
空间复杂度:O(n^2)。我们需要保存每个点上的 4 方向上连续 1 的最小数目即可,需要的空间为 O(n^2)。