【2022-12-19每日一题】1971. 寻找图中是否存在路径[Easy]

2022-12-19每日一题：1971. 寻找图中是否存在路径

难度：Easy

标签：深度优先搜索 、 广度优先搜索 、 并查集 、 图

有一个具有 n 个顶点的 双向 图，其中每个顶点标记从 0 到 n - 1（包含 0 和 n - 1）。图中的边用一个二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和顶点 vi 之间的双向边。 每个顶点对由 最多一条 边连接，并且没有顶点存在与自身相连的边。

请你确定是否存在从顶点 source 开始，到顶点 destination 结束的 有效路径 。

给你数组 edges 和整数 n、source 和 destination，如果从 source 到 destination 存在 有效路径 ，则返回 true，否则返回 false 。

示例 1：

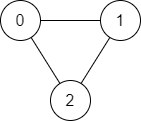
输入：n = 3, edges = [[0,1],[1,2],[2,0]], source = 0, destination = 2
输出：true
解释：存在由顶点 0 到顶点 2 的路径:
- 0 → 1 → 2 
- 0 → 2

示例 2：

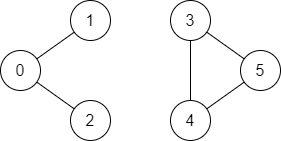
输入：n = 6, edges = [[0,1],[0,2],[3,5],[5,4],[4,3]], source = 0, destination = 5
输出：false
解释：不存在由顶点 0 到顶点 5 的路径.

提示：

• 1 <= n <= 2 * 105
• 0 <= edges.length <= 2 * 105
• edges[i].length == 2
• 0 <= ui, vi <= n - 1
• ui != vi
• 0 <= source, destination <= n - 1
• 不存在重复边
• 不存在指向顶点自身的边

方法一：DFS

func validPath(n int, edges [][]int, source int, destination int) bool {
    if source == destination {
        return true
    }
    conn := make([][]int, n)
    for _, e := range edges {
        x, y := e[0], e[1]
        conn[x] = append(conn[x], y)
        conn[y] = append(conn[y], x)
    }
    vis := make([]bool, n)
    var dfs func(int) bool
    dfs = func(s int) bool {
        if vis[s] {
            return false
        }
        vis[s] = true
        for _, x := range conn[s] {
            if x == destination {
                return true
            }
            if dfs(x) {
                return true
            }
        }
        return false
    }
    return dfs(source)
}

// 大佬写法
func validPath(n int, edges [][]int, source int, destination int) bool {
    vis, conn := make([]bool, n), make([][]int, n)
    for _, e := range edges {
        x, y := e[0], e[1]
        conn[x] = append(conn[x], y)
        conn[y] = append(conn[y], x)
    }
    var dfs func(int) bool
    dfs = func(s int) bool {
        if s == destination {
            return true
        }
        vis[s] = true
        for _, x := range conn[s] {
            if !vis[x] && dfs(x) {
                return true
            }
        }
        return false
    }
    return dfs(source)
}

复杂度分析

• 时间复杂度：$O(n+m)$，其中 n 表示图中顶点的数目，m 表示图中边的数目。
• 空间复杂度：$O(n+m)$，其中 n 表示图中顶点的数目，m 表示图中边的数目。

BFS

func validPath(n int, edges [][]int, source int, destination int) bool {
    vis, conn := make([]bool, n), make([][]int, n)
    for _, e := range edges {
        x, y := e[0], e[1]
        conn[x] = append(conn[x], y)
        conn[y] = append(conn[y], x)
    }
    q := []int{source}
    vis[source] = true
    for len(q) > 0 {
        i := q[0]
        if i == destination {
            return true
        }
        q = q[1:]
        for _, j := range conn[i] {
            if !vis[j] {
                q = append(q, j)
                vis[j] = true
            }
        }
    }
    return false
}

复杂度分析

• 时间复杂度：$O(n+m)$，其中 n 表示图中顶点的数目，m 表示图中边的数目。
• 空间复杂度：$O(n+m)$，其中 n 表示图中顶点的数目，m 表示图中边的数目。

并查集

// find 递归版本
func validPath(n int, edges [][]int, source int, destination int) bool {
    p := make([]int, n)
    for i := range p {
        p[i] = i
    }
    var find func(int) int
    find = func(x int) int {
        if p[x] != x {
            p[x] = find(p[x])
        }
        return p[x]
    }
    for _, e := range edges {
        p[find(e[0])] = find(e[1])
    }
    return find(source) == find(destination)
}

// find 迭代版本
func validPath(n int, edges [][]int, source int, destination int) bool {
    p := make([]int, n)
    for i := range p {
        p[i] = i
    }
    find := func(x int) int {
        for p[x] != x {
            p[x] = p[p[x]]
            x = p[x]
        }
        return x
    }
    for _, e := range edges {
        p[find(e[0])] = find(e[1])
    }
    return find(source) == find(destination)
}

复杂度分析

• 时间复杂度：O(n+m×α(m))，其中 n是图中的顶点数，m 是图中边的数目，α 是反阿克曼函数。并查集的初始化需要 O(n)的时间，然后遍历 m 条边并执行 m 次合并操作，最后对 source 和 destination 执行一次查询操作，查询与合并的单次操作时间复杂度是 O(α(m))，因此合并与查询的时间复杂度是 O(m×α(m))，总时间复杂度是 O(n+m×α(m))。

• 空间复杂度：O(n)，其中 n 是图中的顶点数。并查集需要 O(n) 的空间。

LeetCode题库地址

• https://leetcode.cn/problems/find-if-path-exists-in-graph