【2022-12-14每日一题】1697. 检查边长度限制的路径是否存在[Hard]

2022-12-14每日一题：1697. 检查边长度限制的路径是否存在

难度：Hard

标签：并查集 、 图 、 数组 、 排序

给你一个 n 个点组成的无向图边集 edgeList ，其中 edgeList[i] = [ui, vi, disi] 表示点 ui 和点 vi 之间有一条长度为 disi 的边。请注意，两个点之间可能有 超过一条边 。

给你一个查询数组queries ，其中 queries[j] = [pj, qj, limitj] ，你的任务是对于每个查询 queries[j] ，判断是否存在从 pj 到 qj 的路径，且这条路径上的每一条边都 严格小于 limitj 。

请你返回一个 布尔数组 answer ，其中 answer.length == queries.length ，当 queries[j] 的查询结果为 true 时， answer 第 j 个值为 true ，否则为 false 。

示例 1：

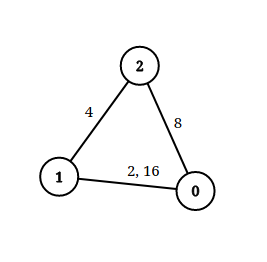
输入：n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
输出：[false,true]
解释：上图为给定的输入数据。注意到 0 和 1 之间有两条重边，分别为 2 和 16 。
对于第一个查询，0 和 1 之间没有小于 2 的边，所以我们返回 false 。
对于第二个查询，有一条路径（0 -> 1 -> 2）两条边都小于 5 ，所以这个查询我们返回 true 。

示例 2：

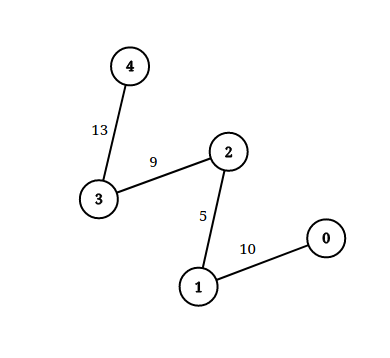
输入：n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]
输出：[true,false]
解释：上图为给定数据。

提示：

• 2 <= n <= 105
• 1 <= edgeList.length, queries.length <= 105
• edgeList[i].length == 3
• queries[j].length == 3
• 0 <= ui, vi, pj, qj <= n - 1
• ui != vi
• pj != qj
• 1 <= disi, limitj <= 109
• 两个点之间可能有 多条 边。

方法一：离线查询+并查集

详细思路过程见官方题解，这里只做个人刷题记录，方便后续查询阅读

func distanceLimitedPathsExist(n int, edgeList [][]int, queries [][]int) []bool {
    // 按边长从小到大排序
    sort.Slice(edgeList, func(i, j int) bool { return edgeList[i][2] < edgeList[j][2] })
    
    // 并查集模板
    fa := make([]int, n)
    for i := range fa {
        fa[i] = i
    }
    var find func(int) int
    find = func(x int) int {
        if fa[x] != x {
            fa[x] = find(fa[x])
        }
        return fa[x]
    }
    merge := func(from, to int) {
        x, y := find(from), find(to)
        fa[x] = y
    }
    // 把索引记录下来
    for i := range queries {
        queries[i] = append(queries[i], i)
    }
    // 按照 limit 从小到大排序，方便离线
    sort.Slice(queries, func(i, j int) bool { return queries[i][2] < queries[j][2] })
    ans, k := make([]bool, len(queries)), 0
    for _, query := range queries {
        // 把小于 limit 的边进行连接
        for ; k < len(edgeList) && edgeList[k][2] < query[2]; k++ {
            merge(edgeList[k][0], edgeList[k][1])
        }
        ans[query[3]] = find(query[0]) == find(query[1])
    }
    return ans
}

复杂度分析

• 时间复杂度：$O(Elog⁡E+mlog⁡m+(E+m)log⁡n+n)$，其中 E 是 edgeList 的长度，m 是 queries 的长度，n 是点数。对 edgeList 和 queries 进行排序分别需要 $O(Elog⁡E)$ 和 $O(mlog⁡m)$，并查集初始化需要 $O(n)$，并查集查询和合并总共需要 $O((E+m)logn)$。

• 空间复杂度：$O(log⁡E+m+n)$。保存并查集需要 $O(n)$ 的空间，保存 index 需要 $O(m)$ 的空间，以及排序需要的栈空间。

LeetCode题库地址

• https://leetcode.cn/problems/checking-existence-of-edge-length-limited-paths