2022-08-05每日一题：623. 在二叉树中增加一行

2022-08-05每日一题：623. 在二叉树中增加一行

给定一个二叉树的根 root 和两个整数 val 和 depth ，在给定的深度 depth 处添加一个值为 val 的节点行。

注意，根节点 root 位于深度 1 。

加法规则如下:

• 给定整数 depth，对于深度为 depth - 1 的每个非空树节点 cur ，创建两个值为 val 的树节点作为 cur 的左子树根和右子树根。
• cur 原来的左子树应该是新的左子树根的左子树。
• cur 原来的右子树应该是新的右子树根的右子树。
• 如果 depth == 1 意味着 depth - 1 根本没有深度，那么创建一个树节点，值 val 作为整个原始树的新根，而原始树就是新根的左子树。

示例 1:

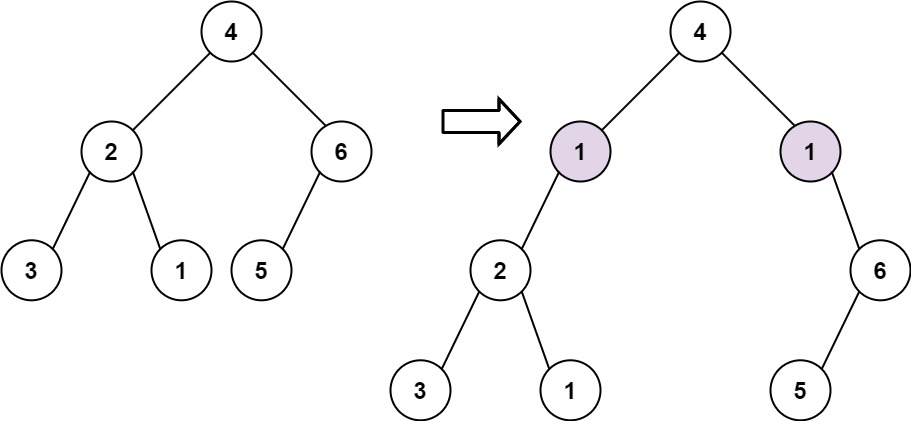
输入: root = [4,2,6,3,1,5], val = 1, depth = 2
输出: [4,1,1,2,null,null,6,3,1,5]

示例 2:

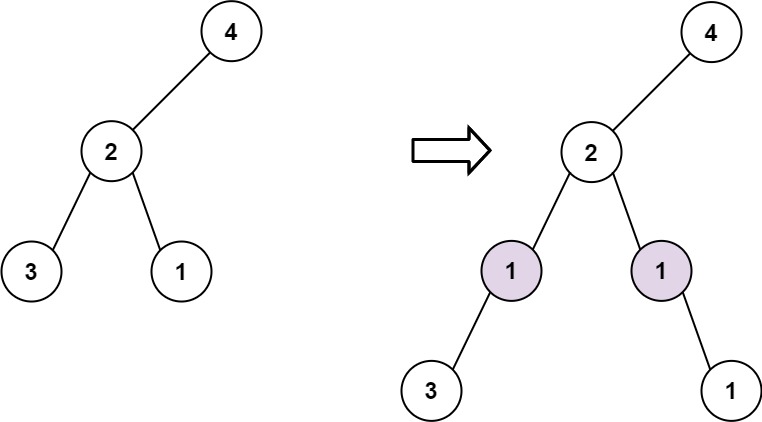
输入: root = [4,2,null,3,1], val = 1, depth = 3
输出:  [4,2,null,1,1,3,null,null,1]

提示:

• 节点数在 [1, 104] 范围内
• 树的深度在 [1, 104]范围内
• -100 <= Node.val <= 100
• -105 <= val <= 105
• 1 <= depth <= the depth of tree + 1

方法一：深度优先遍历

• 当depth 为 1 时，需要创建一个新的 root，并将原 root 作为新 root 的左子节点。

• 当depth 为 2 时，需要在root 下新增两个节点left 和 right 作为root 的新子节点，并把原左子节点作为left 的左子节点，把原右子节点作为 right 的右子节点。

• 当 depth 大于 2 时，需要继续递归往下层搜索，并将 depth 减去 1，直到搜索到 depth 为 2。

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func addOneRow(root *TreeNode, val int, depth int) *TreeNode {
    if root == nil {
        return root
    }
    if depth == 1 {
        return &TreeNode{Val: val, Left: root}
    }
    if depth == 2 {
        root.Left = &TreeNode{Val: val, Left: root.Left}
        root.Right = &TreeNode{Val: val, Right: root.Right}
    } else {
        root.Left = addOneRow(root.Left, val, depth-1)
        root.Right = addOneRow(root.Right, val, depth-1)
    }
    return root
}

复杂度分析

• 时间复杂度：O(n)，其中 n 为输入的树的节点数。最坏情况下，需要遍历整棵树。

• 空间复杂度：O(n)，递归的深度最多为 O(n)。

方法二：深度优先遍历

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func addOneRow(root *TreeNode, val int, depth int) *TreeNode {
    if root == nil {
        return root
    }
    if depth == 1 {
        return &TreeNode{Val: val, Left: root}
    }
    queue := []*TreeNode{root}
    for i := 0; i < depth - 2; i++ {
        for n := len(queue); n > 0; n-- {
            node := queue[0]
            queue = queue[1:]
            if node.Left != nil {
                queue = append(queue, node.Left)
            }
            if node.Right != nil {
                queue = append(queue, node.Right)                
            }
        }
    }
    for _, node := range queue {
        node.Left = &TreeNode{Val: val, Left: node.Left}
        node.Right = &TreeNode{Val: val, Right: node.Right}
    }
    return root
}

复杂度分析

• 时间复杂度：O(n)，其中 n 为输入的树的节点数。最坏情况下，需要遍历整棵树。

• 空间复杂度：O(n))，数组空间开销最多为 O(n)。

LeetCode题库地址

• https://leetcode.cn/problems/add-one-row-to-tree